Gradient Boost Algorithm

Back to: Machine Learning

Gradient Boosting

Gradient Boosting is an ensemble learning method that builds models sequentially, where each new model corrects the errors of the previous ones using gradient descent. It minimizes the loss function by learning from the residuals (errors) of the previous models.

Step-by-Step Process of Gradient Boosting

Step 1: Initialize with a Weak Model

• Start with a simple prediction, often the mean (for regression) or log-odds (for classification).
• Example: If we are predicting house prices, we begin with the average price of all houses.

Step 2: Compute Residuals (Errors)

• Calculate how much each prediction differs from the actual value: Residual=Actual Value−Predicted Value

Step 3: Train a Decision Tree on the Residuals

• Fit a small decision tree (weak learner) to predict these residuals.
• This tree learns how to correct the previous prediction.

Step 4: Compute the New Prediction

• Update the prediction using a learning rate (η): F1(x)=F0(x)+η×Tree1(x)
  • F0(x) is the initial prediction.
  • η is a small value (0.1, 0.01, etc.) to control learning.
  • Tree1(x) s the weak learner trained on residuals.

Step 5: Repeat the Process

• Compute new residuals based on F1(x) and fit another weak learner to correct errors further.
• The process continues for multiple iterations: F2(x)=F1(x)+η×Tree2(x)
• F3(x)=F2(x)+η×Tree3(x)
  • Each step reduces the error by adding another tree that focuses on the residuals.

Step 6: Final Prediction

• The final model is the sum of all weak models: 
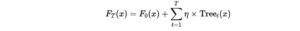
• Each weak learner contributes slightly to the final prediction, gradually improving accuracy.

Example Problem: Predicting House Prices

We have the following dataset:

House Size (sq ft)	House Price (Y)
1000	150
1200	200
1500	250
1800	300
2000	350

Our goal is to predict house prices based on size using Gradient Boosting.

---

Step 1: Initial Prediction (Mean)

The first prediction is the mean of the target variable:

$$=250$$

So, our initial prediction for all houses is 250.

House Size	Actual Price (Y)	Initial Prediction (F₀)	Residual (Y – F₀)
1000	150	250	150 – 250 = -100
1200	200	250	200 – 250 = -50
1500	250	250	250 – 250 = 0
1800	300	250	300 – 250 = 50
2000	350	250	350 – 250 = 100

---

Step 2: Train a Weak Learner (Decision Tree) on Residuals

A small decision tree is trained to predict residuals.

Example Tree Splits:

• If House Size ≤ 1200, predict -75 (average of -100 and -50).
• If House Size > 1200, predict 50 (average of 0, 50, and 100).

House Size	Residual (Y – F₀)	Tree Prediction
1000	-100	-75
1200	-50	-75
1500	0	50
1800	50	50
2000	100	50

---

Step 3: Update Predictions with Learning Rate

Gradient Boosting updates the predictions using:

F1=F0+η×Tree OutputF_1 

where η (learning rate) = 0.1.

House Size	Initial Prediction (250)	Tree Output	Updated Prediction (F₁)
1000	250	-75	250 + (0.1 × -75) = 242.5
1200	250	-75	242.5
1500	250	50	250 + (0.1 × 50) = 255
1800	250	50	255
2000	250	50	255

---

Step 4: Compute New Residuals

Now we compute new residuals:

r1=Y−F1​

House Size	Actual Price (Y)	Updated Prediction (F₁)	New Residual (Y – F₁)
1000	150	242.5	150 – 242.5 = -92.5
1200	200	242.5	200 – 242.5 = -42.5
1500	250	255	250 – 255 = -5
1800	300	255	300 – 255 = 45
2000	350	255	350 – 255 = 95

---

Step 5: Train Another Weak Learner on New Residuals

A new decision tree is trained to predict the new residuals.

Example Tree Splits:

• If House Size ≤ 1200, predict -67.5 (average of -92.5 and -42.5).
• If House Size > 1200, predict 45 (average of -5, 45, and 95).

House Size	New Residual (Y – F₁)	Tree Prediction
1000	-92.5	-67.5
1200	-42.5	-67.5
1500	-5	45
1800	45	45
2000	95	45

---

Step 6: Update Predictions Again

F2=F1+η×Tree Output

House Size	Previous Prediction (F₁)	Tree Output	Updated Prediction (F₂)
1000	242.5	-67.5	242.5 + (0.1 × -67.5) = 235.75
1200	242.5	-67.5	235.75
1500	255	45	255 + (0.1 × 45) = 259.5
1800	255	45	259.5
2000	255	45	259.5

---

Step 7: Compute New Residuals Again

r2=Y−F2​

House Size	Actual Price (Y)	Updated Prediction (F₂)	New Residual (Y – F₂)
1000	150	235.75	150 – 235.75 = -85.75
1200	200	235.75	200 – 235.75 = -35.75
1500	250	259.5	250 – 259.5 = -9.5
1800	300	259.5	300 – 259.5 = 40.5
2000	350	259.5	350 – 259.5 = 90.5

---

Step 8: Repeat Until Convergence

• Train another tree on new residuals.
• Update predictions using learning rate.
• Continue until residuals become small.