AdaBoost(Adaptive Boosting)

Back to: Machine Learning

AdaBoost (Adaptive Boosting) is an ensemble learning algorithm that combines multiple weak learners (usually decision stumps) by iteratively adjusting sample weights to focus on misclassified instances, improving overall model accuracy.

components of AdaBoost (Adaptive Boosting) are:

1. Weak Learners – Simple models (usually decision stumps) that perform slightly better than random guessing.
2. Sample Weights – Each data point is assigned a weight, which is updated in each iteration to focus more on misclassified samples.
3. Error Rate (ε) – The proportion of misclassified samples by each weak learner, used to adjust its influence.
4. Learner Weight (α) – A measure of each weak learner’s importance, computed based on its error rate.
5. Final Hypothesis – A weighted combination of all weak learners, forming a strong classifier.

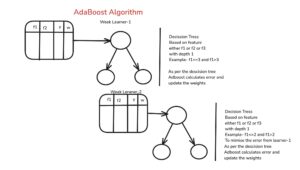
NOTE if AdaBoost uses decision trees as weak learners, the trees typically use Gini index (or entropy) for feature selection.

Mathematical Formula

Let us understand through Data

 

“Should we play tennis today?” based on weather conditions.

 

Step 1: Dataset – “Play Tennis?” Decision

We have 5 days of weather data with the Outlook feature as the decision variable.

Day	Outlook	Play Tennis (y)
1	Sunny	No (-1)
2	Overcast	Yes (+1)
3	Rainy	Yes (+1)
4	Sunny	No (-1)
5	Rainy	Yes (+1)

• Feature: Outlook (Sunny, Overcast, Rainy)
• Target Variable: Play Tennis?
  • Yes (+1)
  • No (-1)

Step 2: Initialize Weights

Initially, all 5 samples get equal weights: 1/5 = 0.2

Day	Outlook	Play Tennis (y)	Initial Weight $w$
1	Sunny	No (-1)	0.2
2	Overcast	Yes (+1)	0.2
3	Rainy	Yes (+1)	0.2
4	Sunny	No (-1)	0.2
5	Rainy	Yes (+1)	0.2

Step 3: Train the First Weak Learner (Decision Stump)

We create a simple rule that tries to separate classes.

Rule 1: If Outlook is Overcast → Predict Yes (+1), Else → Predict No (-1)

Day	Outlook	True Class (y)	Prediction	Correct?
1	Sunny	No (-1)	No (-1)	✅ Correct
2	Overcast	Yes (+1)	Yes (+1)	✅ Correct
3	Rainy	Yes (+1)	No (-1)	❌ Wrong
4	Sunny	No (-1)	No (-1)	✅ Correct
5	Rainy	Yes (+1)	No (-1)	❌ Wrong

Misclassified days: Day 3, Day 5
Total weight of errors: ϵ1=0.2+0.2=0.4

Step 4: Compute Learner Weight α1\alpha_1α1​

α1=12ln⁡(1−ϵ1ϵ1)\alpha_1 = \frac{1}{2} \ln \left( \frac{1 – \epsilon_1}{\epsilon_1} \right)α1​=21​ln(ϵ1​1−ϵ1​​) α1=12ln⁡(1−0.40.4)=12ln⁡(1.5)\alpha_1 = \frac{1}{2} \ln \left( \frac{1 – 0.4}{0.4} \right) = \frac{1}{2} \ln \left( 1.5 \right)α1​=21​ln(0.41−0.4​)=21​ln(1.5) α1=12×0.405=0.202\alpha_1 = \frac{1}{2} \times 0.405 = 0.202α1​=21​×0.405=0.202

This means the first weak learner contributes to the final model with weight 0.202.

---

Step 5: Update Weights

• Misclassified samples get more weight to make them more important in the next iteration.
• Updated weight formula:

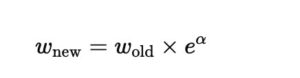
Day	Outlook	Old Weight $w$	Misclassified?	New Weight w
1	Sunny	0.2	❌ No	0.167
2	Overcast	0.2	❌ No	0.167
3	Rainy	0.2	✅ Yes	0.267
4	Sunny	0.2	❌ No	0.167
5	Rainy	0.2	✅ Yes	0.267

Observation

• Misclassified (Day 3, Day 5) weights increased from 0.2 → 0.267
• Correctly classified samples’ weights reduced from 0.2 → 0.167

Step 6: Train Second Weak Learner

A new weak learner now pays more attention to Rainy days because they have higher weight.

Rule 2: If Outlook is Rainy → Predict Yes (+1), Else → Predict No (-1)

Day	Outlook	True Class (y)	Prediction	Correct?
1	Sunny	No (-1)	No (-1)	✅ Correct
2	Overcast	Yes (+1)	No (-1)	❌ Wrong
3	Rainy	Yes (+1)	Yes (+1)	✅ Correct
4	Sunny	No (-1)	No (-1)	✅ Correct
5	Rainy	Yes (+1)	Yes (+1)	✅ Correct

Misclassified day: Day 2
Error weight:ϵ2=0.167

 

Step 7: Compute Learner Weight α2

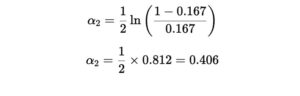
Step 8: Update Weights Again

• Day 2 (misclassified) gets a weight increase.
• Other days have adjusted weights.

Day	Outlook	Old Weight w′	Misclassified?	New Weight w′′
1	Sunny	0.167	❌ No	0.143
2	Overcast	0.167	✅ Yes	0.286
3	Rainy	0.267	❌ No	0.229
4	Sunny	0.167	❌ No	0.143
5	Rainy	0.267	❌ No	0.229