Back to: Machine Learning
Distance Metrics for Classification in Machine Learning
Distance metrics play a vital role in machine learning, especially in classification tasks like k-Nearest Neighbors (k-NN), clustering, and similarity-based algorithms.
They help quantify the “closeness” or “similarity” between data points. In this blog, we will explore various distance metrics, their mathematical formulas, real-time examples, and manual calculations.
Key Distance Metrics
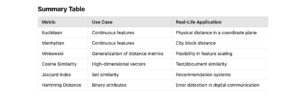
- Euclidean Distance
- Manhattan Distance
- Minkowski Distance
- Cosine Similarity
- Jaccard Index
- Hamming Distance
Sample Dataset
Here’s a sample dataset representing customers and their attributes:
| Customer ID | Age (Years) | Income (in $1000s) | Spending Score (0-100) |
|---|---|---|---|
| C1 | 25 | 50 | 85 |
| C2 | 30 | 55 | 80 |
| C3 | 35 | 60 | 70 |
| C4 | 40 | 65 | 60 |
1. Euclidean Distance
The straight-line distance between two points in a multidimensional space.

2. Manhattan Distance
The sum of the absolute differences between dimensions.

3. Minkowski Distance
A generalized distance metric that includes both Euclidean and Manhattan distances.

4. Cosine Similarity
Measures the cosine of the angle between two vectors.

5. Jaccard Index
Used for comparing the similarity between two sets.

6. Hamming Distance
Measures the difference between two binary strings.